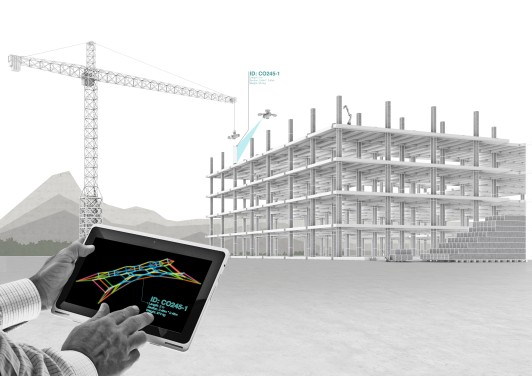
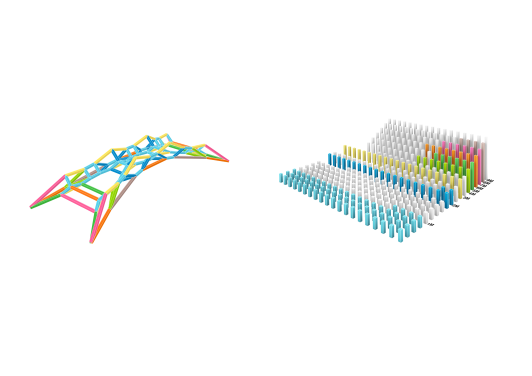
The extensive use of concrete in construction plays a massive role in carbon emission. Current recycling strategies rather downcycle concrete by grinding building elements for future use in road construction. This thesis aims to create a new approach for reusing the old concrete components through Graphic-Statics, Best-Fitting algorithms, and robotic-aided fabrication.
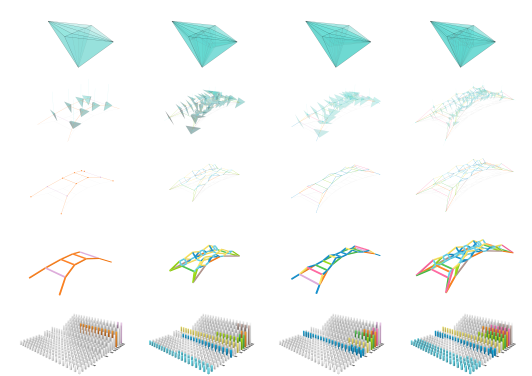
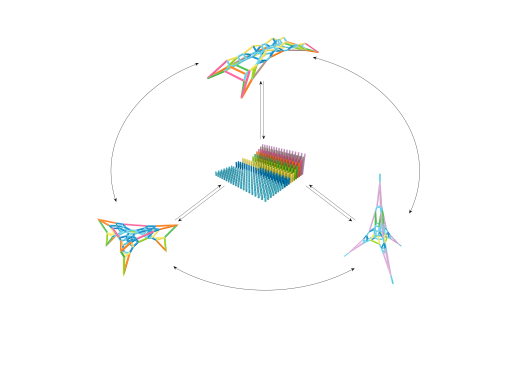
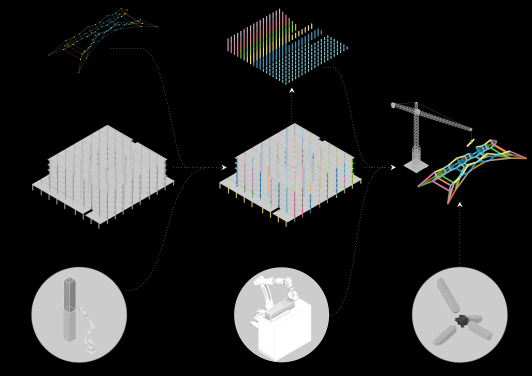
3d Graphic-Statics is used to design compression-only concrete skeleton structures that do not rely on potentially unknown steel reinforcement of existing building elements. A computational design process that integrates form-finding, discrete optimization, and robotic toolpath planning has been developed. The strategy is exemplified by redistributing used components onto three different structural typologies: The bridge, the tower, the roof. The system shows how old concrete components can be reused without losing its grey energy and all the time, effort and resources of designing them.
Empfohlener externer Content
Wir haben für Sie einen externen Inhalt von YouTube ausgewählt und möchten Ihnen diesen hier zeigen. Dazu müssen Sie ihn mit einem Klick einblenden. Mit einem weiteren Klick können Sie den externen Inhalt jederzeit ausblenden.
Ich bin damit einverstanden, dass mir externe Inhalte von YouTube angezeigt werden. Dadurch ist es möglich, dass personenbezogene Daten an Drittplattformen übermittelt werden. Weitere Informationen finden Sie in unserer Datenschutzerklärung.
Empfohlener externer Content
Wir haben für Sie einen externen Inhalt von YouTube ausgewählt und möchten Ihnen diesen hier zeigen. Dazu müssen Sie ihn mit einem Klick einblenden. Mit einem weiteren Klick können Sie den externen Inhalt jederzeit ausblenden.
Ich bin damit einverstanden, dass mir externe Inhalte von YouTube angezeigt werden. Dadurch ist es möglich, dass personenbezogene Daten an Drittplattformen übermittelt werden. Weitere Informationen finden Sie in unserer Datenschutzerklärung.
Empfohlener externer Content
Wir haben für Sie einen externen Inhalt von YouTube ausgewählt und möchten Ihnen diesen hier zeigen. Dazu müssen Sie ihn mit einem Klick einblenden. Mit einem weiteren Klick können Sie den externen Inhalt jederzeit ausblenden.
Ich bin damit einverstanden, dass mir externe Inhalte von YouTube angezeigt werden. Dadurch ist es möglich, dass personenbezogene Daten an Drittplattformen übermittelt werden. Weitere Informationen finden Sie in unserer Datenschutzerklärung.
Empfohlener externer Content
Wir haben für Sie einen externen Inhalt von YouTube ausgewählt und möchten Ihnen diesen hier zeigen. Dazu müssen Sie ihn mit einem Klick einblenden. Mit einem weiteren Klick können Sie den externen Inhalt jederzeit ausblenden.
Ich bin damit einverstanden, dass mir externe Inhalte von YouTube angezeigt werden. Dadurch ist es möglich, dass personenbezogene Daten an Drittplattformen übermittelt werden. Weitere Informationen finden Sie in unserer Datenschutzerklärung.
Graphic statics, yields structures with compression-only and tension-only members. To realize such a structure with an existing stock of building elements we need to calculate the optimal combination of the existing components. The quantity of the used components defines the amount of possible combinations. Solutions are discrete and discontinuous. Therefore typical optimization algorithms like the Genetic Algorithm are inappropriate to solve the problem because they are geared towards solving continuous mathematical optimization problems. In computer science, our challenge of assigning building elements to new positions in compression-only structures is called an assignment problem: „The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows:
The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment. It is required to perform as many tasks as possible by assigning at most one agent to each task and most one task to each agent, in such a way the total cost of the assignment is minimized.“
According to the above definition of this problem, the redistribution problem can be translated into an assignment problem. Therefore the used components are correspondingly defined as agents, and every line segment in the structure will be a task. To evaluate the redistributed result‘s fitness, according to the assignment problem‘s definition, every agent‘s efficiency value (given component) on every task (input component) should be quantified. Efficiency here is defined as the difference between the given com¬ponents‘ and the input components‘ length which is defined as the efficiency matrix. The Hungarian method is used as combinatorial optimization algorithm for this task.
Robotic Sawing
To fabricate the joints between the reused elements a robot arm is used to saw the components. With the robot arm‘s implementation, different kinds of connections are easily customizable providing of the high degree of geometric freedom and providing high accuracy. Different kinds of connections of the components have been explored and tested with a various tool such as milling machine, bandsaw, circular saw.
Supervision: Bastian Wibranek, Oliver Tessmann
References
Akbarzadeh, M., Mahnia, M., Taherian, R. and Hossein, A.: 2017, Prefab , Concrete Polyhedral Frame : Materializing 3D Graphic Statics, Proceedings of IASS 2017, Hamburg, 8-11
Brütting, J., Senatore, G., & Fivet, C. (2019). Form follows availability–Designing structures through reuse. Journal of the International Association for Shell and Spatial Structures, 60(4), 257-265.
Hablicsek, M., Akbarzadeh, M., & Guo, Y. (2019). Algebraic 3D graphic statics: Reciprocal constructions. Computer-Aided Design, 108, 30-41.
Lee, J. (2018). Computational Design Framework for 3D Graphic Statics (Doctoral dissertation, ETH Zurich).
Dry Joint Column, ITE Braunschweig, https://www.youtube.com/watch?v=XREXHn1NrC8&t=6s&ab_channel=ITE-TUBraunschweig, accessed 05.06.2020